জার্মান বিজ্ঞানী কারশফ তড়িৎ বর্তনী সংক্রান্ত যে দুটি সূত্র প্রণয়ন করেন, সেগুলি কারশফের সূত্র নামে পরিচিত। কারশফের সূত্রের সাহায্যে খুব সহজেই তড়িৎ বর্তনীতে প্রবাহমাত্রা এবং বিভব প্রভেদ সংক্রান্ত বিভিন্ন গাণিতিক সমস্যার সহজ সমাধান করা যায়।
জটিল বর্তনীর বিভিন্ন অংশের প্রবাহমাত্রা এবং বিভবপ্রভেদ গণনা করার জন্য কারশফের সূত্র (কার্শফের সূত্র) খুবই উপযোগী।
প্রকৃতপক্ষে কারশফের সূত্র নতুন কোন সূত্র নয়, এটি ওহমের সূত্রেরই পরিবর্তিত রূপ।
কারশফের প্রথম সূত্র:
কারশফের প্রথম সূত্র – বিবৃতি:
তড়িৎ বর্তনী যেকোনো জংশন বিন্দুতে প্রবেশ করা এবং জংশন বিন্দু থেকে বেরিয়ে যাওয়া মোট তড়িৎ প্রবাহমাত্রার বীজগাণিতিক যোগফল শূন্য হয়।
কারশফের প্রথম সূত্র – ব্যাখ্যা:
চিত্রে, একটি জংশন বিন্দু দেখানো হয়েছে। ছবিটিতে দেখা যাচ্ছে, ওই জংশন বিন্দুতে I1, I2 এবং I3 – তিনটি প্রবাহ প্রবেশ করেছে এবং I4 প্রবাহ জংশন বিন্দু থেকে বেরিয়ে গিয়েছে।
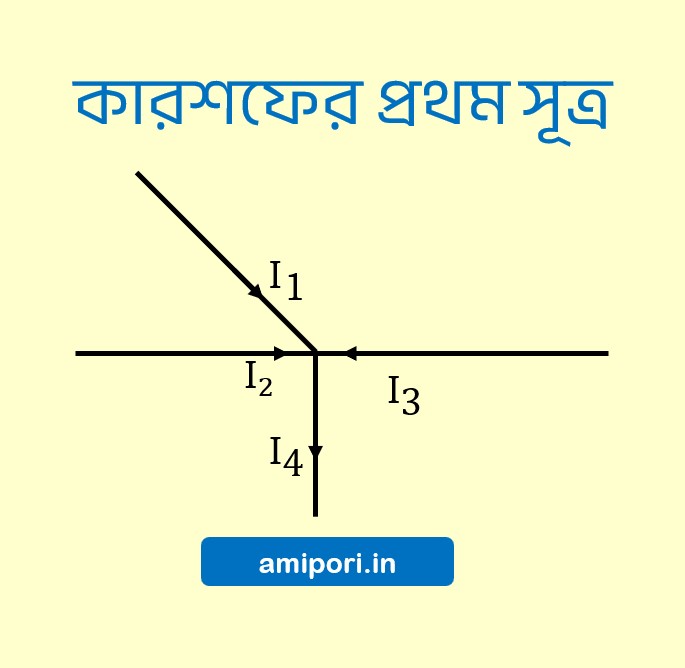
কারশফের প্রথম সূত্র অনুসারে উক্ত চিত্রের ক্ষেত্রে বলা যায়,
I1+I2+I3=I4
or, I1+I2+I3-I4 = 0
অর্থাৎ, কারশফের প্রথম সূত্র থেকে বলা যায়,
জংশনে প্রবেশ করা মোট কারেন্ট = জংশন থেকে বেরিয়ে যাওয়া মোট কারেন্ট
গাণিতিক ভাবে একে এভাবেও লেখা যায়,
Σ জংশনে প্রবেশ করা কারেন্ট / প্রবাহ = Σ জংশন থেকে বেরিয়ে যাওয়া কারেন্ট প্রবাহ
Σ iin = Σ iout
(যেখানে, iin = জংশনে প্রবেশ করা কারেন্ট এবং iout = জংশন থেকে বেরিয়ে যাওয়া কারেন্ট
কারশফের প্রথম সূত্র সম্পর্কে বিস্তারিত জানার জন্য এখানে ক্লিক করুন –
কারশফের প্রথম সূত্র
কারশফের দ্বিতীয় সূত্র:
কারশফের দ্বিতীয় সূত্র – বিবৃতি:
তড়িৎ বর্তনীতে যেকোনো বদ্ধ লুপের ক্ষেত্রে প্রতিটি রোধ এবং তার সঙ্গে সংশ্লিষ্ট প্রবাহমাত্রার গুণফল ওই লুপের মোট কার্যকরী তড়িচ্চালক বলের মানের সমান হয়।

