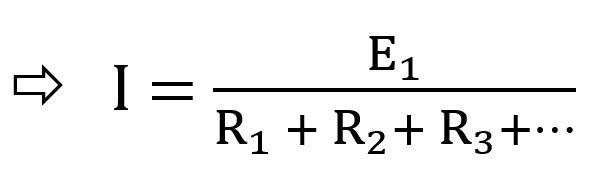কারশফ তড়িৎ বর্তনী সংক্রান্ত যে দুটি সূত্র প্রণয়ন করেন তাদেরকে কারশফের সূত্র বলা হয়ে থাকে।
ইতিমধ্যে কারশফের প্রথম সূত্র বিষদে ব্যখ্যা করা হয়েছে,আগ্রহী ছাত্রছাত্রীরা এখান থেকে কারশফের প্রথম সূত্র বিষদে জানতে পারবে।
এই দুটি সূত্রের মধ্যে দ্বিতীয় সূত্র অর্থাৎ কারশফের দ্বিতীয় সূত্র নিচে বিশদে ব্যাখ্যা করা হল।
কারশফের দ্বিতীয় সূত্র – বিবৃতি:
তড়িৎ বর্তনীতে যেকোনো বদ্ধ লুপের ক্ষেত্রে প্রতিটি রোধ এবং তার সঙ্গে সংশ্লিষ্ট প্রবাহমাত্রার গুণফল ওই লুপের মোট কার্যকরী তড়িচ্চালক বলের মানের সমান হয়।
কারশফের দ্বিতীয় সূত্রকে অনেক সময় কারশফের ভোল্টেজ সূত্র বা Kirchhoff’s Voltage Law বা সংক্ষেপে KVL -ও লেখা হয়।
⭐ কারশফের দ্বিতীয় সূত্র শক্তির সংরক্ষণ নীতির ওপর প্রতিষ্ঠিত বা এই সূত্র শক্তির সংরক্ষণ নীতিকে সমর্থন করে।
এবিষয়ে বিস্তারিত জানার জন্য এই নিবন্ধটি দেখুন –
কারশফের দ্বিতীয় সূত্র থেকে শক্তির সংরক্ষণ সূত্র
কারশফের দ্বিতীয় সূত্র – ব্যাখ্যা:
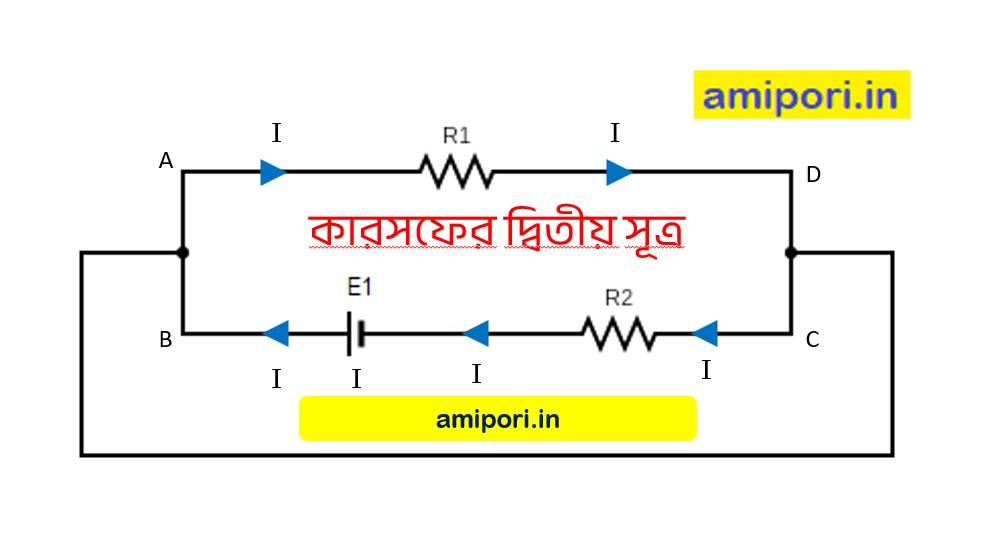
ওপরের চিত্রটিতে দেখা যাচ্ছে, ABCDA নামক একটি লুপ নেওয়া হয়েছে, যাতে R1 এবং R2 নামক দুটি রোধ (যাদের দ্বারা বর্তনীতে ভোল্টেজ / বিভবপ্রভেদের অপচয় ঘটছে) এবং E1 নামের একটি সেল (Cell) রয়েছে – যারা দ্বারা লুপটিতে I মানের প্রবাহ উৎপন্ন হচ্ছে, যার ফলে বিভবপ্রভেদের সৃষ্টি হচ্ছে।
ধরা যাক, E1 কোশ থেকে I মানের প্রবাহ উৎপন্ন হচ্ছে এবং যেহেতু লুপটিতে ১ টি মাত্র কোশ রয়েছে, তাই লুপটিতে I মানের প্রবাহ-ই প্রবাহিত হচ্ছে।
অতএব, R1 এবং R2 রোধদুটি কর্তৃক বিভবপতন –
R1 কর্তৃক বিভবপতন = IR1
R2 কর্তৃক বিভবপতন = IR2
অতএব, লুপটিতে মোট বিভবপতন = IR1 + IR2
আবার, E1 cell কর্তৃক উৎপন্ন তড়িৎচালক বল = E1
বর্তনীতে উৎপন্ন মোট তড়িৎচালক বল = E1
অতএব, ABCDA নামক লুপটির ক্ষেত্রে, কারশফের দ্বিতীয় সূত্র থেকে সিদ্ধান্তে আসা যায়,
IR1 + IR2 = E1
কারশফের দ্বিতীয় সূত্র – গাণিতিক রূপ:
Σ লুপে উৎপন্ন বিভবপ্রভেদ = Σ লুপের মোট বিভবপতন
Σ E1 + E2 + E3 + …. = Σ IR1 + IR2 + IR3 + …
Σ E = Σ IR ……………. (i)
[যেখানে, E = লুপে উৎপন্ন মোট বিভবপ্রভেদ, I = প্রবাহমাত্রা, R = তুল্য রোধের মান]
(i) নং সমীকরণটিকে কারশফের দ্বিতীয় সূত্র গাণিতিক রূপ বলা যেতে পারে।
কারশফের দ্বিতীয় সূত্র সম্পর্কিত কয়েকটি তথ্য
👉 কারশফের দ্বিতীয় সূত্র কারশফের ভোল্টেজ সূত্র ছাড়াও কারশফের লুপ সূত্র নামেও পরিচিত।
👉 কারশফের প্রথম সূত্র যেমন আধান সংরক্ষণের নীতির উপর প্রতিষ্ঠিত তেমনই কারশফের দ্বিতীয় সূত্র শক্তি সংরক্ষণ নীতির ওপর প্রতিষ্ঠিত।
👉 কারশফের প্রথম সূত্রের মত দ্বিতীয় সূত্রও ওখানে সূত্র থেকেই তৈরি হয়েছে এবং এটিও নতুন কোন সূত্র নয়।
কারশফের দ্বিতীয় সূত্রের প্রয়োগ
কারশফের দ্বিতীয় সূত্র প্রয়োগ করে জটিল বর্তনীতে লুপ তৈরি করে সহজেই প্রতিটি লুপে প্রবাহমাত্রা গণ্না করা যায়। নীচে ১ কোশ (cell) বিশিষ্ট লুপে এই সূত্র প্রয়োগ করে প্রবাহমাত্রা গণনা করে দেখানো হল –
গাণিতিকভাবে কারশফের দ্বিতীয় সূত্রের প্রয়োগ ১ cell বিশিষ্ট লুপে প্রবাহমাত্রা গণনা
আমরা জানি,
IR1 + IR2 + IR3 + … = E1
–> I(R1 + R2 + R3 + …) = E1