যদি
আমরা জানি,
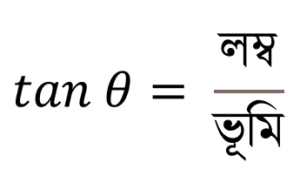
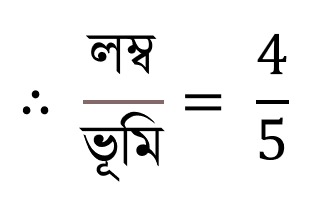
ধরা যাক, লম্ব = একক এবং ভূমি =
একক
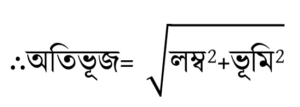
∴ অতিভূজ একক

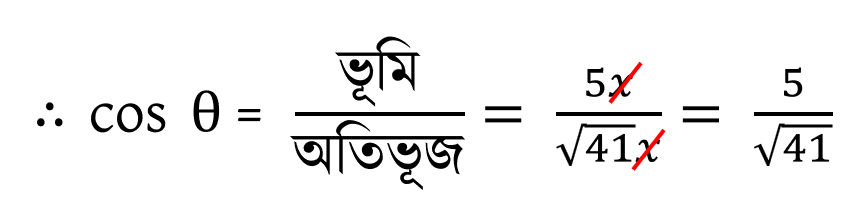
∴
প্রদত্ত রাশিমালায় এবং
এর মান বসিয়ে পাই,
(Answer)
যদি
আমরা জানি,
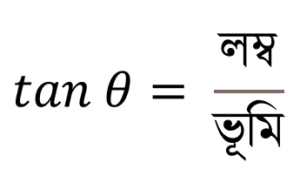
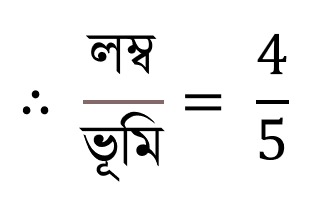
ধরা যাক, লম্ব = একক এবং ভূমি =
একক

∴ অতিভূজ একক

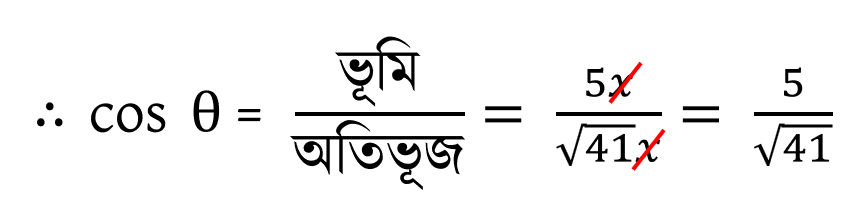
∴
প্রদত্ত রাশিমালায় এবং
এর মান বসিয়ে পাই,
(Answer)