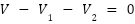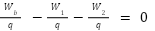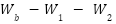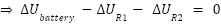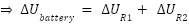জটিল তড়িৎ বর্তনীর বিভিন্ন অংশে প্রবাহমাত্রা এবং বিভব প্রভেদ সহজে নির্ণয়ের জন্য বিজ্ঞানী কারশফ যে দুটি সূত্র দিয়েছিলেন, সেগুলি নিয়ে ইতিমধ্যে আগের পোস্টগুলিতে আলোচনা করা হয়েছে।
এর মধ্যে কারশফের দ্বিতীয় সূত্রকে শক্তির সংরক্ষণ সূত্রও বলা হয়ে থাকে।
কারশফের দ্বিতীয় সূত্রকে কেন শক্তির সংরক্ষণ সূত্রও বলা হয় এবং কারশফের দ্বিতীয় সূত্র থেকে শক্তির সংরক্ষণ সূত্র কীভাবে পাওয়া সে নিয়ে নিয়ে আলোচনা করা হল –
কারশফের দ্বিতীয় সূত্র বা কারশফের ভোল্টেজ সূত্র থেকে পাওয়া যায়,
ΣΔV = 0
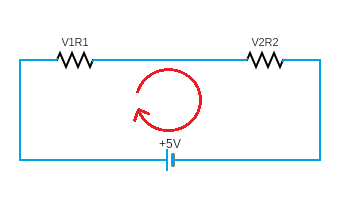
উপরের তড়িৎ বর্তনী (সার্কিট) – এ এই সূত্র প্রয়োগ করে পাওয়া যায় –