কারশফ তড়িৎ বর্তনী সংক্রান্ত যে দুটি সূত্র প্রণয়ন করেন তাদেরকে কারশফের সূত্র বলা হয়ে থাকে।
এই দুটি সূত্রের মধ্যে প্রথম সূত্র অর্থাৎ কারশফের প্রথম সূত্র নিচে বিশদে ব্যাখ্যা করা হল।
কারশফের প্রথম সূত্র – বিবৃতি:
তড়িৎ বর্তনী যেকোনো জংশন বিন্দুতে প্রবেশ করা এবং জংশন বিন্দু থেকে বেরিয়ে যাওয়া মোট তড়িৎ প্রবাহমাত্রার বীজগাণিতিক যোগফল শূন্য হয়।
কারশফের প্রথম সূত্রকে অনেক সময় কারসফের কারেন্ট সূত্র বা Kirchhoff’s Current Law বা সংক্ষেপে KCL -ও লেখা হয়।
কারশফের প্রথম সূত্র – ব্যাখ্যা:
চিত্রে, একটি জংশন বিন্দু দেখানো হয়েছে। ছবিটিতে দেখা যাচ্ছে, ওই জংশন বিন্দুতে I1, I2 এবং I3 – তিনটি প্রবাহ প্রবেশ করেছে এবং I4 প্রবাহ জংশন থেকে বেরিয়ে গিয়েছে।
(জংশন – বর্তনীর যেই বিন্দুতে ৩ এর বেশি তার / বর্তনীর যেকোনো অংশ একসঙ্গে মিলিত হয়, সেই বিন্দুকে জংশন বলা হয়।)
অর্থাৎ, কারশফের প্রথম সূত্র থেকে বলা যায়,
জংশনে প্রবেশ করা মোট কারেন্ট = জংশন থেকে বেরিয়ে যাওয়া মোট কারেন্ট
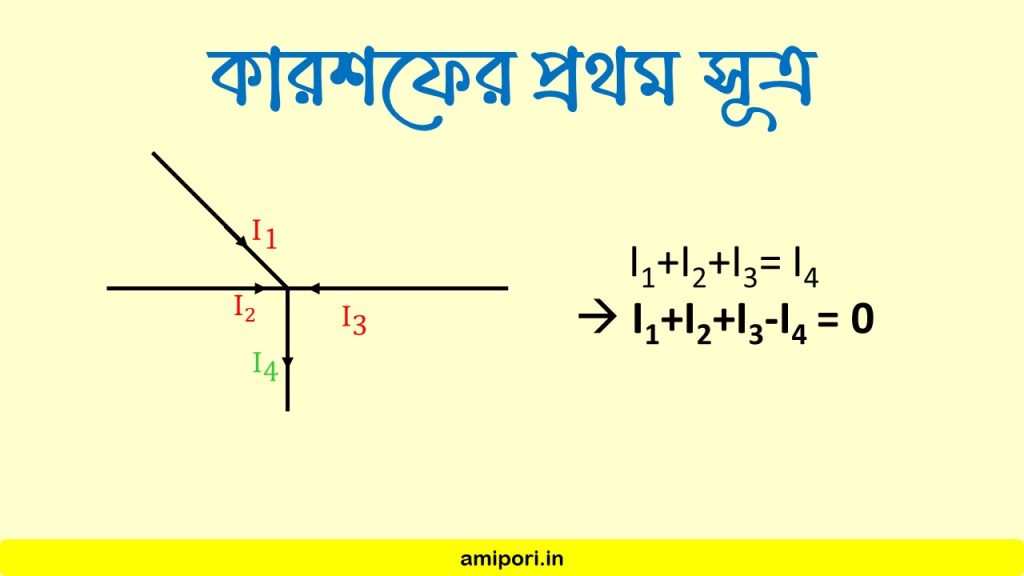
প্রথম সূত্র অনুসারে উক্ত চিত্রের ক্ষেত্রে বলা যায়,
I1+I2+I3=I4
or, I1+I2+I3-I4 = 0
গাণিতিক ভাবে একে এভাবেও লেখা যায়,
Σ জংশনে প্রবেশ করা কারেন্ট / প্রবাহ = Σ জংশন থেকে বেরিয়ে যাওয়া কারেন্ট প্রবাহ
Σ iin = Σ iout
(যেখানে, iin = জংশনে প্রবেশ করা কারেন্ট এবং iout = জংশন থেকে বেরিয়ে যাওয়া কারেন্ট)
কারশফের প্রথম সূত্র সম্পর্কিত কয়েকটি তথ্য
👉 কারশফের প্রথম সূত্র সমপ্রবাহ (Direct Current) এবং পরিবর্তী প্রবাহ (Alternating Current) এই দুই প্রকার প্রবাহের ক্ষেত্রেই প্রযোজ্য। (উল্লেখ্য: পরিবর্তী প্রবাহের জন্য কারশফের প্রথম সূত্র এর প্রয়োগের ক্ষেত্রে জটিল সংখ্যা (Complex Number) এর ব্যবহার দেখা যায়)
👉সমান্তরাল এবং শ্রেণী – উভয় প্রকার সমবায়ের ক্ষেত্রে কারশফের প্রথম সূত্র প্রযোজ্য হয় এবং সঠিক গণনা দ্বারা উভয়প্রকার সমবায়ের ক্ষেত্রেই কারশফের প্রথম সূত্র প্রয়োগ করে সহজেই বর্তনীর সমাধান করা যায়।
