দেখাও x2−6x+8=0 সমীকরণের একটি বীজ অপরটির বর্গ

Leave a Comment / Class 10 Math, Class 10 / By

প্রদত্ত সমীকরণটি হল – x2−6x+8=0
প্রমাণ করতে হবে, একটি বীজ অপরটির বর্গ

⇒ x2− (4+2)x + 8=0
⇒ x2−4x -2x + 8=0
⇒ x(x-4) -2(x-4) = 0
⇒ (x-4) (x-2) = 0

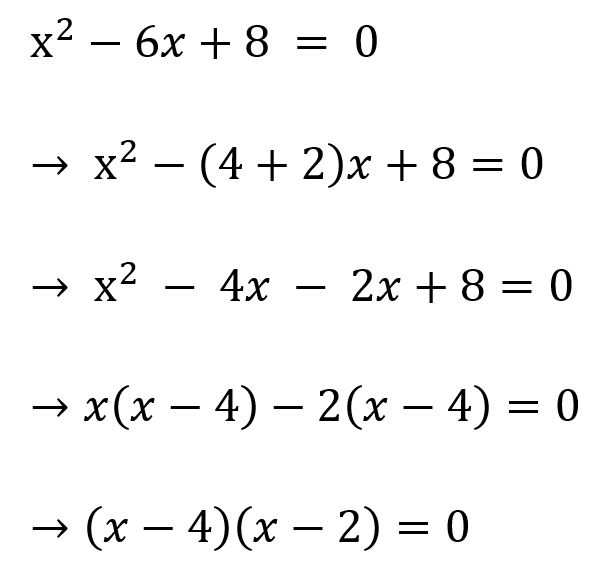
\begin{array}{l} x^2-6x+8=0\\ \rightarrow\ x^2-\left(4+2\right)x+8=0\\ \rightarrow x^2\ -\ 4x\ -\ 2x+8=0\\ \rightarrow x\left(x-4\right)-2\left(x-4\right)=0\\ \rightarrow\left(x-4\right)\left(x-2\right)=0 \end{array}

হয়, x – 4 = 0
∴ x = 4
নাহলে, x – 2 = 0
∴ x = 2

সমীকরণটির ২ টি বীজ পাওয়া গেল, যথা – 2 ও 4
স্পষ্টতই, বীজ দুটি একে ওপরের বর্গ [যেহেতু, 4 = 22]
∴ x2−6x+8=0 সমীকরণের একটি বীজ অপরটির বর্গ – প্রমাণিত

Leave a Comment

Your email address will not be published. Required fields are marked *