কোনো তড়িৎবর্তনীতে একাধিক রোধ উপস্থিত থাকলে, মূলত ২ ভাবে তাদের সমবায় ঘটানো যায় –
- ১। শ্রেণি সমবায়
- ২। সমান্তরাল সমবায়
শ্রেণি সমবায় সম্পর্কে পূর্ববর্তী পোষ্টে আগেই আলোচনা করা হয়েছে, এই পোষ্টে রোধের সমান্তরাল সমবায় নিয়ে আলোচনা করা হবে।
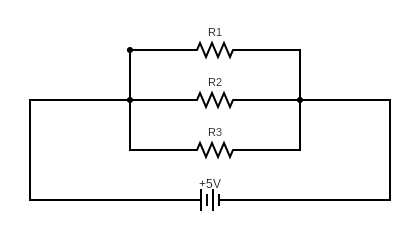
কতকগুলি রোধক যদি এমনভাবে যুক্ত থাকে যে, প্রতিটি রোধের এক প্রান্ত এক স্থানে এবং অপর প্রান্ত অপর স্থানে যুক্ত থাকে, তবে সেই প্রকার সমবায়কে রোধের সমান্তরাল সমবায় বলা হয়।
সমান্তরাল সমবায়ের তুল্য রোধের গাণিতিক রাশিমালা
ধরা যাক, R1, R2, R3 তিনটি রোধ সমান্তরাল সমবায়ে যুক্ত আছে।
এখন, ঐ রোধ সমবায়ের তুল্য রোধ Re ধরা হলে, লেখা যায়,
Re কথাটির মানে হল Equivalent Resistance (e – equivalent) [Equivalent = তুল্য]
n টি রোধের ক্ষেত্রে রোধের সমান্তরাল সমবায়ের সূত্র
কোনো রোধ সমবায়ে n টি রোধ সমান্তরাল সমবায়ে যুক্ত থাকলে, যদি তুল্য রোধ Re হয়, তবে লেখা যায়,
রোধের সমান্তরাল সমবায় এর বৈশিষ্ট্য
১। রোধের শ্রেণি সমবায় এর ক্ষেত্রে সমবায়ের প্রতিটি রোধের বিভবপ্রভেদ সমান হয় কিন্তু প্রবাহমাত্রা আলাদা আলাদা হয় ৷
২। রোধের শ্রেণি সমবায়ের ক্ষেত্রে তুল্য রোধের অন্যোন্যকের মান সকল রোধের অন্যোন্যকের মানের যোগফলের সমান হয়। এজন্য এই সমবায়ে তুল্য রোধের মান যেকোনো রোধের তুলনায় কম হয়।
